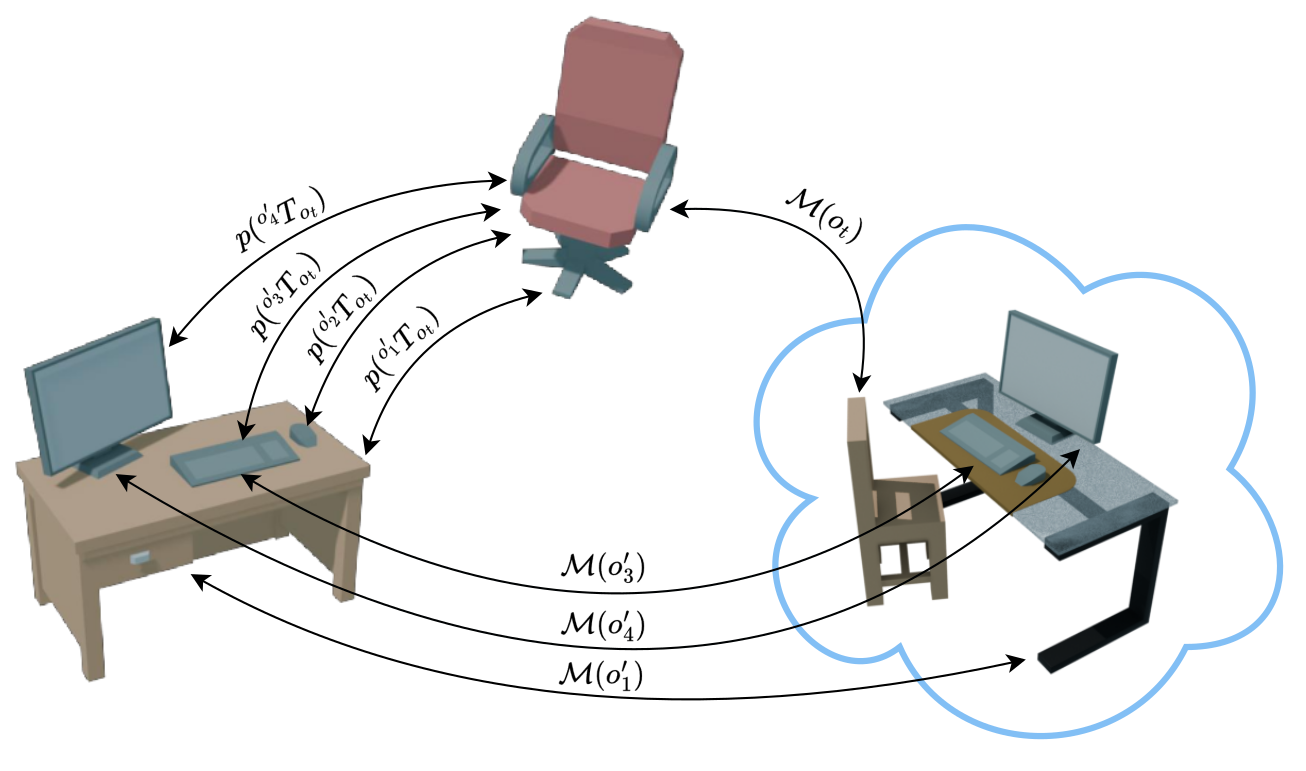
In this work, we investigate the problem of sequential object placement, which assumes that a sequence of objects $\O_p = \set{o_1, \ldots, o_n}$ needs to be placed in a scene in relation to a static set of objects $\O_s$. Each placed object transitions from $\O_p$ to $\O_s$. Formally: At time step $t = 1$, the sets are the initial sets $\O_p$ and $\O_s$, afterwards they change to $\O_{p,t} = \set{o_t, \ldots, o_n}$ and $\O_{s,t} = \O_s \cup \set{o'_1, \ldots, o'_{t-1}}$ for all $t \leq n$.
Each object $o$ has a world-space pose $\tf{W}{T}{o}$ and a class $c_o$. Each class is associated with a set of feature points, $\F_c = \set{(e_1, p_1), \ldots, (e_m, p_m)}$ which consist of an embedding $e \in \R^E$ and a position $p \in \R^3$ in a canonical class frame. The generation of feature points and their utility for manipulation and pose estimation and tracking is widely studied in robotics.
Given this structure, we seek to learn the distribution of object placements in the scene, given its class, and the poses and classes of the other already placed objects: $\probcdist{t}{\tf{W}{T}{o_t}}{c_{o_t}, c_{o'_1}, \ldots, c_{o'_{t-1}}, \tf{W}{T}{o'_1}, \dots \tf{W}{T}{o'_{t-1}}}$, with $o'_1, \ldots, o'_{t-1} \in \O_{s,t}$.
In order to learn poses effectively, we decompose of learning world space poses $\probcdist{t}{\tf{W}{T}{o_t}}{\ldots}$ into
\[
\begin{aligned}
\probcdist{t}{\tf{W}{T}{o_t}}{c_{o_t}, c_{o'_1}, \ldots, c_{o'_{t-1}}, \tf{W}{T}{o'_1}, \dots \tf{W}{T}{o'_{t-1}}} &= \prod_{o' \in \O_{s,t}} \probcdist{t}{\tf{o'}{T}{o_t}}{c_{o_t}, c_{o'}},
\end{aligned}
\]
learning of relative poses $\tf{o'}{T}{o}$, which we derive as $\tf{o'}{T}{o} = \tf{W}{T}{o'}^{-1}\cdot\tf{W}{T}{o}$. To enable intra-category transfer, we assume there exists an invertible class mapping $\M(o) = o_c$ which maps an object's properties, \ie its pose and feature points, to the canonical categorical representation. This yields the probability of a relative pose given the observed distribution of poses in categorical space as
\[
\begin{aligned}
\probcdist{t}{\tf{o'}{T}{o_t}}{c_{o_t}, c_{o'}} &= \probc{\tf{o'}{T}{o_t}}{\M(o')\tf{o'}{T}{o} \M(o_t)}. % \propto \N (\vec{\mu}, \vec{\sigma} )
\end{aligned}
\]
Class maps deform an instance of an object to best match a known canonical object. Our approach requires these maps to be affine transformations, but in this work we only consider linear scaling instances.
To learn the relative poses of objects in category space, we use multivariate normal distributions. Our distributions capture the relative pose $\tf{b}{\hat{T}}{a}$ of two objects $a, b$ where
$\tf{b}{\hat{T}}{a} = \M_b \tf{b}{T}{a}$, with $\M_b$ being the class mapping for the object $b$.
While $\tf{b}{\hat{T}}{a} \in \R^{4\times4}$ is a convenient representation for computations, it does not lend itself to learning due to its size and redundancy. Instead, we represent these poses in a lower-dimensional feature space. We represent the encoding into this space as an invertible function $f$. We consider a number of options for $f$, but also study choosing $f$ based on the entropy of the resulting distribution.
Especially in larger scenes, many of the relative pose observations will not be relevant to the placement of an object and might even be distracting. Imagine placing a cup on a coffee table that is set in front of a sofa. While the relative pose of cup and sofa will have a statistical trend, semantically, this correlation is (largely) spurious. When performing inference, maintaining all of these relationships potentially increases the number of samples needing to be drawn and the numerical instability. Thus, given the fitted distributions $\probdist{o_1}{\tf{o_1}{T}{o_t}}, \ldots, \probdist{o_{t-1}}{\tf{o_{t-1}}{T}{o_t}}$, we seek to identify the minimal set of distributions $O^*_{s,t} \subseteq \O_{s,t}$ which represents the data. We propose doing so by using an outlier-discrimination strategy.
Please refer to our paper for more details.